Introduzione al Teorema di Bayes

Il Teorema di Bayes è un potente strumento che ci aiuta a capire come la nostra conoscenza previa, detta probabilità a priori, possa essere aggiornata con nuove informazioni, dette probabilità condizionate, per ottenere una probabilità a posteriori più accurata. In parole povere, il teorema ci dice come possiamo aggiornare le nostre credenze sulla base di nuove prove.
Spiegazione del Teorema di Bayes
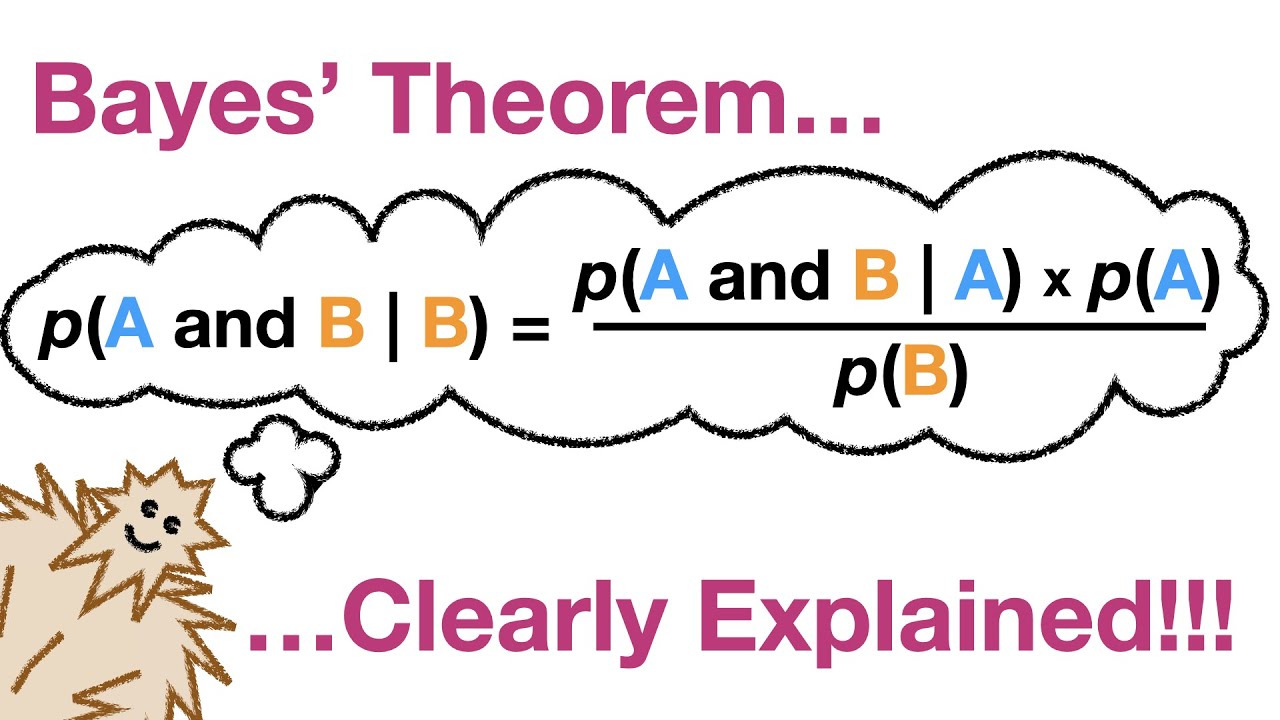
Il teorema di Bayes è espresso dalla seguente formula:
P(A|B) = [P(B|A) * P(A)] / P(B)
Dove:
* P(A|B) è la probabilità dell’evento A dato che l’evento B si è verificato.
* P(B|A) è la probabilità dell’evento B dato che l’evento A si è verificato.
* P(A) è la probabilità a priori dell’evento A.
* P(B) è la probabilità a priori dell’evento B.
Esempio Concreto
Immagina di avere un test medico per una malattia. Il test è abbastanza preciso, ma non perfetto. Supponiamo che il test abbia un tasso di falsi positivi del 5% (cioè, il 5% delle persone sane risulta positivo al test) e un tasso di falsi negativi del 10% (cioè, il 10% delle persone malate risulta negativo al test).
Ora, supponiamo che tu abbia fatto il test e il risultato è positivo. Qual è la probabilità che tu abbia effettivamente la malattia?
Per rispondere a questa domanda, possiamo usare il teorema di Bayes.
* P(Malattia|Positivo) è la probabilità di avere la malattia dato che il test è positivo.
* P(Positivo|Malattia) è la probabilità di ottenere un risultato positivo al test dato che si ha la malattia (1 – tasso di falsi negativi = 90%).
* P(Malattia) è la probabilità a priori di avere la malattia (questa è una stima basata sulla popolazione generale).
* P(Positivo) è la probabilità a priori di ottenere un risultato positivo al test (questa può essere calcolata considerando il tasso di falsi positivi e la prevalenza della malattia nella popolazione).
Applicando il teorema di Bayes, possiamo calcolare la probabilità di avere la malattia dato che il test è positivo.
Importanza del Teorema di Bayes
Il teorema di Bayes è fondamentale per la probabilità e l’inferenza statistica perché ci permette di aggiornare le nostre conoscenze in base a nuove informazioni. Questo è particolarmente utile quando si tratta di situazioni incerte o con dati limitati.
Applicazioni del Teorema di Bayes
Il teorema di Bayes ha un’ampia gamma di applicazioni in diversi campi, tra cui:
* Medicina: Per diagnosticare malattie e valutare l’efficacia dei trattamenti.
* Finanza: Per analizzare i rischi e prevedere i rendimenti degli investimenti.
* Intelligenza artificiale: Per sviluppare sistemi di apprendimento automatico e intelligenza artificiale.
* Scienza forense: Per valutare la probabilità di una corrispondenza tra un sospettato e un’evidenza.
* Marketing: Per analizzare i dati dei clienti e migliorare le campagne pubblicitarie.
* Meteorologia: Per prevedere il tempo e valutare la probabilità di eventi meteorologici estremi.
* Sicurezza informatica: Per rilevare intrusioni e attività dannose nei sistemi informatici.
Concetti Fondamentali: Bayesian
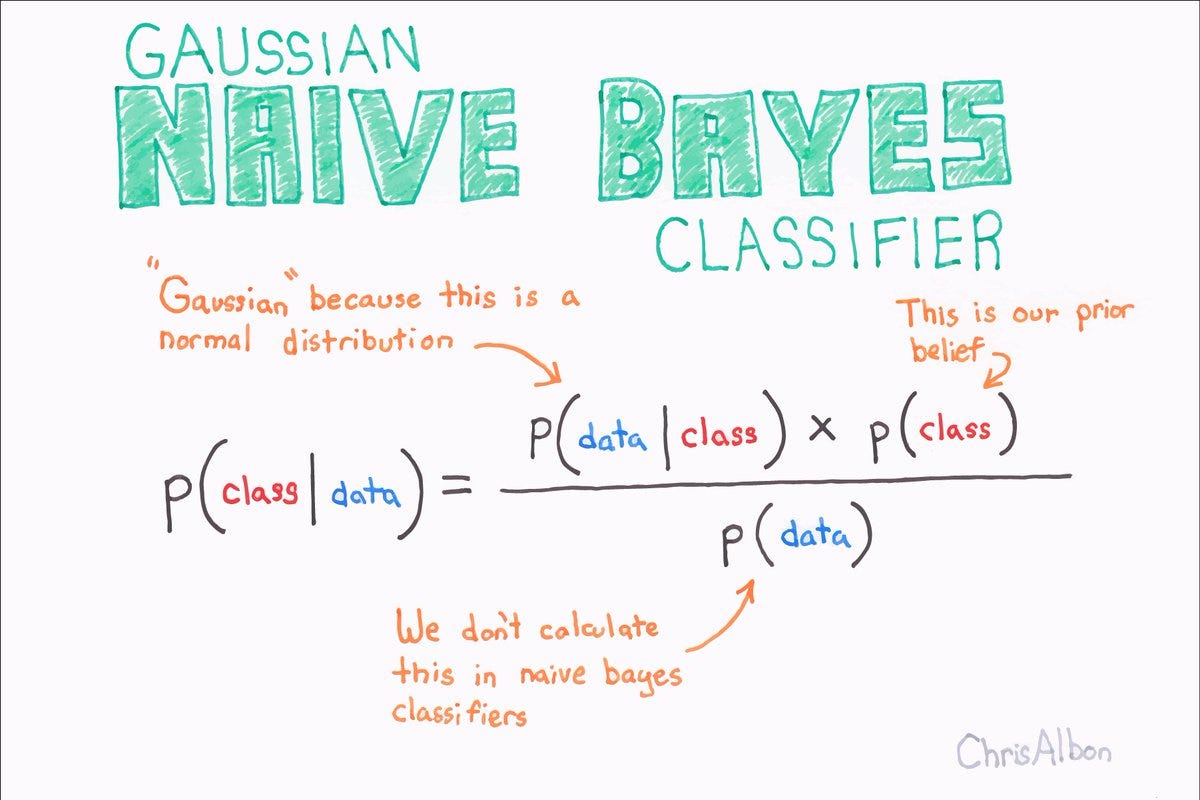
Il teorema di Bayes si basa su concetti chiave che aiutano a comprendere il suo funzionamento e la sua applicazione in vari ambiti. Questi concetti, che sono interconnessi tra loro, forniscono il framework per analizzare le probabilità e le relazioni tra eventi.
Probabilità a priori, probabilità a posteriori, probabilità condizionata e probabilità marginale
Questi termini chiave sono fondamentali per comprendere il teorema di Bayes.
- Probabilità a priori: rappresenta la probabilità di un evento prima di osservare nuove informazioni o dati. È una misura della nostra conoscenza o credenza iniziale su un evento. Ad esempio, la probabilità a priori di ottenere testa lanciando una moneta è 1/2, poiché assumiamo che la moneta sia equa.
- Probabilità a posteriori: rappresenta la probabilità di un evento dopo aver osservato nuove informazioni o dati. È una misura della nostra conoscenza aggiornata sull’evento dopo aver considerato le nuove evidenze. Ad esempio, se lanciamo una moneta 10 volte e otteniamo testa 7 volte, la probabilità a posteriori di ottenere testa sarà maggiore di 1/2, poiché le nuove evidenze suggeriscono che la moneta potrebbe essere sbilanciata.
- Probabilità condizionata: rappresenta la probabilità di un evento A dato che l’evento B è già accaduto. È la probabilità di A condizionata a B. Ad esempio, la probabilità di ottenere testa lanciando una moneta dato che la moneta è sbilanciata è diversa dalla probabilità di ottenere testa lanciando una moneta equa.
- Probabilità marginale: rappresenta la probabilità di un evento senza considerare altre informazioni o eventi. È la probabilità di un evento considerato da solo. Ad esempio, la probabilità marginale di ottenere testa lanciando una moneta è 1/2, indipendentemente da qualsiasi altra informazione.
Relazione tra probabilità a priori e probabilità a posteriori
La probabilità a priori e la probabilità a posteriori sono interconnesse. La probabilità a priori è il punto di partenza per il calcolo della probabilità a posteriori. Le nuove informazioni o dati vengono utilizzati per aggiornare la probabilità a priori e ottenere la probabilità a posteriori.
La probabilità a posteriori è la probabilità a priori aggiornata in base alle nuove informazioni.
Relazione tra il teorema di Bayes e la regola di Bayes
Il teorema di Bayes è una formula matematica che consente di calcolare la probabilità a posteriori di un evento. La regola di Bayes è una formulazione del teorema di Bayes che esprime la probabilità a posteriori in termini di probabilità a priori, probabilità condizionata e probabilità marginale.
La regola di Bayes è un’applicazione pratica del teorema di Bayes.
Applicazioni del Teorema di Bayes
Il teorema di Bayes è un potente strumento che trova applicazione in diverse aree della scienza, della tecnologia e della vita quotidiana. Essenzialmente, questo teorema ci permette di aggiornare le nostre convinzioni sulla probabilità di un evento, basandoci su nuove informazioni.
Diagnosi Medica, Bayesian
Il teorema di Bayes è ampiamente utilizzato in ambito medico per la diagnosi delle malattie. Ad esempio, un medico potrebbe utilizzare il teorema di Bayes per calcolare la probabilità che un paziente abbia una determinata malattia, dato il risultato di un test diagnostico.
- Supponiamo che un test per una malattia abbia una sensibilità del 90% (cioè, il test è positivo nel 90% dei casi in cui la malattia è presente) e una specificità del 95% (cioè, il test è negativo nel 95% dei casi in cui la malattia è assente).
- Se il test di un paziente risulta positivo, il medico può utilizzare il teorema di Bayes per calcolare la probabilità che il paziente abbia effettivamente la malattia, tenendo conto della prevalenza della malattia nella popolazione.
In questo caso, il teorema di Bayes aiuta il medico a prendere una decisione più informata riguardo al trattamento del paziente.
Filtro Antispam
Il teorema di Bayes è utilizzato anche nei filtri antispam per distinguere tra email legittime e spam.
- I filtri antispam utilizzano il teorema di Bayes per calcolare la probabilità che un’email sia spam, basandosi su determinate caratteristiche dell’email, come le parole chiave, l’indirizzo del mittente e il formato dell’email.
- Ad esempio, se un’email contiene molte parole chiave associate allo spam, come “gratis”, “offerta” o “casino”, il filtro antispam potrebbe assegnare una probabilità più alta che l’email sia spam.
Il teorema di Bayes consente ai filtri antispam di migliorare la loro accuratezza nel bloccare lo spam e nel consentire l’accesso alle email legittime.
Classificazione di Documenti
Il teorema di Bayes viene applicato anche nella classificazione di documenti, come ad esempio la categorizzazione di articoli di notizie o di post sui social media.
- In questo caso, il teorema di Bayes viene utilizzato per calcolare la probabilità che un documento appartenga a una determinata categoria, basandosi sul contenuto del documento.
- Ad esempio, un sistema di classificazione di documenti potrebbe utilizzare il teorema di Bayes per determinare se un articolo di notizie appartiene alla categoria “politica”, “sport” o “economia”.
Il teorema di Bayes consente ai sistemi di classificazione di documenti di migliorare la loro accuratezza nel classificare i documenti in base al loro contenuto.
